Number theory in TeX-way
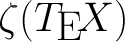Demonstrate some of the features of writing TeX macros, embedded in TeX calculator number-theoretic functions. problem Statement
From time to time I have to type another text, followed by examples of computations of number-theoretic functions: function Euler φ, function τ dividers, the Carmichael λ function. Previously, this was done like this: run your favorite calculator (my choice — PARI/GP), all believe in it and copy the calculations in Those. Changed the original data back to the calculator and back. A lot of fuss, a lot of chances to forget to replace some intermediate result. And just the mouse to swing bored. Want to automate this process for at least the most common functions, so you can write
the
$\phi(1001)=\Phi(1001)$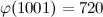
The most common solution is to use an external preprocessor, which would eat it the desired fragments of formulae, put them outside the calculator, take the result and insert it into the document. The main disadvantage is the loss of compatibility. Before, we could just send a tex file through email. Now, to the other end it can be compiled to pdf, and need more detailed instructions, specifying the required preprocessor and calculator. At this stage, we will almost certainly learn that the recipient has a different OS and our dances with a tambourine he gift is not necessary. On to plan B.
Plan B
Try to use their own funds Tex macros which is known to be Turing-complete language. He's not as esoteric as Brainfuck, but very far from si-like syntax and, even worse semantics.
The first thing to notice is that the macro can accept arguments, but can not transparently return values. Packlist would say that the macro does not behave like a function and as a procedure. For example, you can write a macro to add two numbers:
the
\newcount\s\def\addition#1#2{\s=#1\advance\s by#2 \number\s}Confusing? Let's try this again, only with comments and spaces:
the
\newcount\s % declare a numeric variable
\def\addition#1#2{ % declare the macro with two arguments
\s=the#1 % s placed in the first argument
\advance\s by#2 % add second argument
\number\s % to be printed as the number
}Now
the
2+3=\addition{2}{3}(a few More examples of mathematical functions)
the integer quotient
Let's write something more complex. Our first goal — a function that checks whether it is divisible one number by another without a remainder.
the
\newif\ifdivisible % declare the Boolean variable
\newcount\testMod@n % declare a numeric variable
\def\testMod#1#2{ % declare the macro with two arguments
\testMod@n=#1% put in testMod@n the first argument
\divide\testMod@n by#2 % share divisible by the second argument
\multiply\testMod@n by#2% and multiply by it
\ifnum#1=\testMod@n % if the result is again the first argument
\divisibletrue % so balance was not
\else % otherwise
\divisiblefalse % were
\fi%
}This macro puts in the truth divisible, if the division went without a trace, and false otherwise. Check:
the
\testMod{6}{3}
\ifdivisible 1 \else 0 \fi
\testMod{6}{4}
\ifdivisible 1 \else 0 \fi should give the output "1 0": 6 is divisible by 3 but not divisible by 4.
If you saved this code to a file and assembled with tex you probably already saw the error "TeX capacity exceeded". The fact that we forgot to ask you to consider @ as a normal character allowed in the names of macros and variables. This can be done with the command
\catcode `\@11In General, Those know how to work with scopes of variables and macros, but it does so much wrong, as is customary in conventional programming languages. For example, try
\def\addition{\newcount\s}\catcode `\@12Code testing \testMod
Unitary divider and exponentiation
Next step: build a macro that computes the maximum degree of one number, which still divides another evenly (if d is easy it is a unitary divisor):
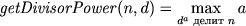
the
\newcount\divisorpower % here we will store the current value and
\newcount\getDivisorPower@m % and here - n/d^a
\def\getDivisorPower#1#2{
\getDivisorPower@m=#1 % initialize variables
\divisorpower=0 %
\testMod{\getDivisorPower@m}{#2} % check whether it is divisible by d
\loop\ifdivisible % while loop that checks the condition divisible
\advance\divisorpower by1 % increment a by 1
\divide\getDivisorPower@m by#2 % divided by d
\testMod{\getDivisorPower@m}{#2} % again check whether it is divisible by d
\repeat % go back to the beginning of the cycle
}In C this code would look like (write it intentionally ugly):
the
int divisible;
int a;
int m;
void getDivisorPower(int n, int d){
m = n;
a = 0;
divisible = (m % d == 0);
while(divisible){
a++;
m /= d;
divisible = (m % d == 0);
}
}Now a little macro:
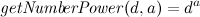
the
\newcount\numberpower % here we will store the result of exponentiation
\newcount\getNumberPower@pow % and here is how many times you multiply it
\def\getNumberPower#1#2{
\numberpower=1 % initialize variables
\getNumberPower@pow=#2
\loop\ifnum\getNumberPower@pow>0 % run cycle
\multiply\numberpower by#1
\advance\getNumberPower@pow by 1
\repeat
}Again in C:
the
int numberpower;
int pow;
void getNumberPower(int d, int a){
numberpower = 1;
pow = a;
while(pow > 0){
numberpower *= d;
pow--;
}
}Could be implemented a more efficient algorithm exponentiation, but we'll settle for this.
It's time to do the test:
the
\getDivisorPower{600}{2}
\number\divisorpower
\getDivisorPower{600}{3}
\number\divisorpower
\getDivisorPower{600}{5}
\number\divisorpower
\getDivisorPower{600}{7}
\number\divisorpowershould print "3 1 2 0" and
the
\getNumberPower{5}{0}
\number\numberpower
\getNumberPower{6}{1}
\number\numberpower
\getNumberPower{7}{2}
\number\numberpowerwill give "1 6 49".
Code testing \getDivisorPower and \getNumberPower
What next?
Part 2 in which we will build a macro, consider the function Euler. For the impatient — working version of the macro. Those can easily handle the calculations for n~109.
Part 3 which will be more clever examples of mathematical calculations in Tex and of course benchmarks.
Комментарии
Отправить комментарий